Çok disiplinli yaklaşımla çeyrek taşıt modelinin modellenmesi

Süspansiyon sistemi, otomobil sürüş konforunu ve stabilitesini iyileştirmek için yoldan gelen darbe yüklerini azaltabilen, taşıtların en önemli parçalarından biridir. Otomobilin konforunu ve dengesini incelemek için çok bilinen ve kullanışlı modellerden biri, otomobilin dörtte birinden (tek tekerlek) oluşan çeyrek taşıt modeli süspansiyon sistemidir. Elbette bu modelde bazı varsayımlar benimsenmiştir, ancak bu, dinamik sistemi kullanan çok sayıda mühendislik uygulamasını etkilemez.

Dinamik sistem modelleme ile ilgilenenler için, bu yazıda sayısal araçların kullanılmasının onları çözmek için ne kadar yararlı olabileceğini gösteren üç farklı yaklaşım gösterilecektir. Bu yöntemleri göstermek için otomotiv dünyasında bilinen bir model olan çeyrek taşıt modeli kullanılacak ve tüm çözümleri tek bir platformda birleştirmenin mümkün olduğu gösterilecektir. Yaklaşımlar şunlardır:

1-) Sinyal tabanlı diyagram (Altair Activate)
2-) Fiziksel tabanlı diyagram (Altair Activate)
3-) 3D mekanik sistem modelleme (Altair MotionSolve)

Dinamik bir sistemi modellemenin başlangıç noktası, sistemi oluşturan cisimlerin davranışını (yer değiştirme, hız, ivme) anlamaktır. Modeli tanımlamak için genellikle serbestlik derecelerini (atalet ve eylemsizlik eksenlerinden) inceleriz. Sistem parçaları ve bağlantı parçaları (rijit, yaylar, damperler) sistemi birbirinden ayırmak ve her birinin ayrı ayrı modellenmesini kolaylaştırmak için izole edilmiştir, daha sonra tüm sistemi temsil etmek için birbirine bağlanacaktır.

Bu, sistemin nasıl çalıştığını ve diferansiyel denklemlerle (doğrusal veya doğrusal olmayan) nasıl temsil edileceğini anlamak için bir mühendis için çok önemli bir görevdir. Bu denklemler, kullanılacak yaklaşımdan bağımsız olarak sistem modellemesinin çekirdeğini oluşturacaktır.

Çeyrek Taşıt modelinin dinamiği

Çeyrek taşıt sistemi, iki cismin olduğu iki serbestlik dereceli bir sistemdir: Yaylı (araba) ve Yaysız (süspansiyon, tekerlek, lastik) kütle. Basitleştirilmiş bir model olmasına rağmen, (fiziksel bir modelde temsili olmayan) her şeyi rijit olarak kabul etmemek için sistemlerin rijitliği ve sönümü kullanılır. Böylece yol ile süspansiyon arasında, lastiğin ve tekerleğin sertliği ve sönümlemesi, süspansiyon ile otomobil arasında ise yay ve amortisörün sertliği ve sönümü dikkate alınır.

Modeli doğrulamak için bilinen bazı parametreler kullanılmıştır. Aktif aktüatörler olmadan pasif bir sistem kullanılan aşağıdaki şekil detayları göstermektedir:

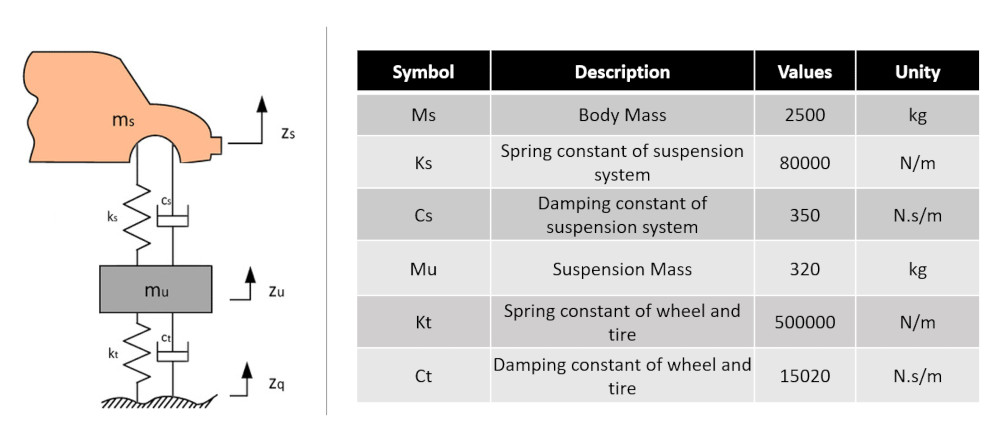
Sistemin diferansiyel denklemlerinin olduğu yerde (serbest cisim diyagramı ile elde edilir):

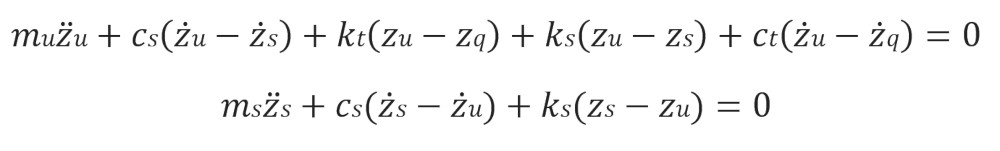
Her bir serbestlik derecesinin başlangıç koşullarının sıfır olacağı ve yol yer değiştirmesi olduğunda girdinin Zq olacağı iki ikinci mertebeden denklem vardır. Pratik amaçlar için bir Adım Girişi (Step Input) kullanılmıştır, bu yazının amacı, sistemi farklı yaklaşımlar kullanarak modellemenin ve çözmenin mümkün olduğunu göstermektir. Bu nedenle temelde her yaklaşım, ortamından bağımsız olarak (0D, 1D veya 3D), istenen değişkenimiz olan Zs‘yi (arabanın yer değiştirmesi) elde etmek için yukarıdaki diferansiyel denklemleri çözecektir, bu sürücüye ve yolculara konfor sağlamak için daha da geliştirilebilir.

1-) Sinyal tabanlı diyagram (Altair Activate)

1D sinyal tabanlı bir ortamda modellemek için kullanılan strateji, denklemleri eklemek ve sonunda en yüksek dereceli değişkeni elde etmek için terimlere bölmektir (bu durumda yaylı ve yaysız kütlenin yer değiştirmesi). Unutulmamalıdır ki, aralarında bağımlı değişkenler bulunduğundan, onları ayrıştırarak çözmenin bir yolu yoktur. Ancak modelleme için bu, yapılması en kolay yöntemdir.

Zaten en yüksek dereceli değişkeni elde etmek için genellikle en büyük toplamlarla başlanır ve bunları değişkenin kendisini oluşturan döngülerde kullanılır. Bu biraz soyut bir yöntemdir, ancak bir blok diyagramda önceki denklemleri oluşturmak için hesaplanacak değişkeni kullanmalısınız. Çeyrek taşıt sisteminin Altair Activate yazılımında oluşturulan blok şeması aşağıda gösterilmiştir (her değişkenin ekseni ve sinyallerinin serbest gövde diyagramınıza bağlı olduğunu unutmayınız):

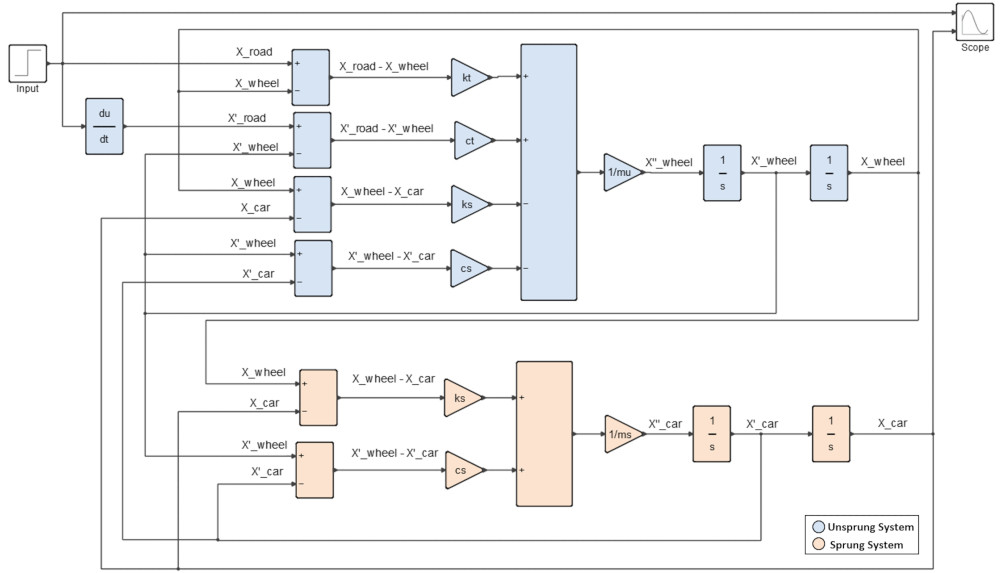
Elbette bir durum-uzay bloğu kullanabilir, bu seçenekle birlikte basit bir 0D script dosyası kullanarak çözebilirsiniz veya script dosyasında daha derine inmek istiyorsanız, ode45 fonksiyonunu, yani Runge-Kutta yöntemini kullanabilirsiniz. Ancak 1D sinyal tabanlı bu tür sistem düşüncesini modellemenin daha normal yolunu göstermek için basit bloklar kullanarak geliştirilmiştir.

2-) Fiziksel tabanlı blok diyagramı (Altair Activate)

Modelica, karmaşık sistemlerin fiziksel tabanlı modellemesi için, nesne yönelimli, çoklu alanlı (multi-domain) bir modelleme dilidir. Kullanıcılar, matematiksel modeli temsil eden basit blokları kullanarak fiziksel sistemleri temsil edebilir, bu şekilde bloklar doğrudan bağlanabilir ve özellikleri kolayca ayarlanabilir. Uygulanan birkaç blok vardır: Mekanik, elektrik, hidrolik, termal, kontrol vb.

Günümüzde Modelica, Altair Activate ile entegre edilmiştir, bu nedenle hibrit bir model (sinyal tabanlı ve fiziksel tabanlı bloklar) sadece basit bir “dönüştürücü (converter)” bloğu (aşağıda giriş ve çıkış blokları arasında temsil edilmektedir) kullanılarak uygulanabilir.

Modellemesi gerçekten çok basit ve bizim sadece gerçek fiziksel model bileşenleri üzerinde düşünmemiz gerekiyor. Yukarıdaki şekilde görülebileceği gibi, bu, Modelin arkasındaki Quarter car – Dynamics‘te bulunan ilk şeklin tam olarak yatay temsilidir, sadece yer değiştirme girdisini ve ölçümü temsil eden bazı bloklar ekleyerek ( bu bizim istenen değişkenimizdir, denklem tarafından Zs).

3-) 3D Mekanik Sistem Modelleme (Altair MotionSolve)

3D mekanik sistemin modellemesi (Altar MotionSolve), parçalar, yaylar, damperler, girişler ve çıkışların dahil edilmesi gerektiği anlamında Modelica ortamındaki modellemeye çok benzer. Ancak sistemin doğru çalışabilmesi için bazı unsurların eklenmesi ve kurulumların yapılması gerektiği unutulmamalıdır.

3D modellemede kurulum anlamında büyük bir özgürlük vardır, yani her bileşen başlangıçta 6 serbestlik derecesine sahiptir. Bu anlamda, bileşenlere doğru çalışma serbestlik derecelerini sağlamak için bazı kısıtlamalar (mafsallar) eklenmelidir.

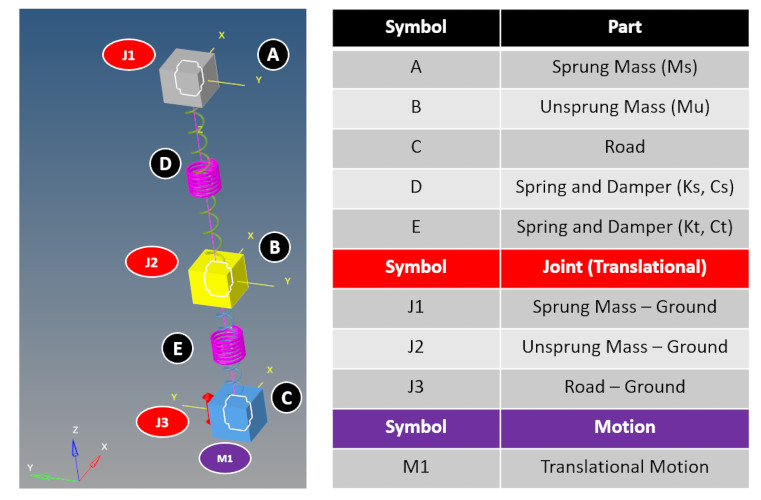
Sonuçlar

Tüm sistemler kendi platformlarında modellendikten sonra Altair Activate kullanılarak entegre edilebilirler. Aşağıdaki video bunu göstermektedir.

Beklendiği gibi, üç sonucun tümü (Zs – araba yer değiştirmesi) temelde aynıdır, yazının başında önerilen, farklı yaklaşımlar kullanarak dinamik bir sistemi modellemek ve çözmek olan şeyi yerine getirir.

Ücretsiz – Altair Activate & Altair MotionSolve öğrenci versiyonu –> İNDİRİN

Kurumsal kullanıcılar için süre kısıtlamalı İNDİRİN– Altair Activate & Altair MotionSolve

Ücretsiz E-kitap (97 sayfa) : Altair Activate ile Sistem Modelleme ve Kontrol Sistemlerinin Temelleri –> İNDİRİN