Doğrusal etkili görsel açıklamaların gücü
Öngörülen gücün ölçümü , hangi girdilerin modelimiz üzerinde en fazla etkiye sahip olduğunu belirlememizi sağlamaktadır. Daha basit bir ifadeyle, “girdiler çıktıları nasıl etkiler?” sorusuna cevap bulmamıza yardımcı olmaktadır. Fisher ve Pierce’ın ilk çalışmalarından sonraki Taguchi ve Box gibi uygulayıcılara kadar, deney tasarımlarındaki ana fikir, bir girdi değişkeninin etkisi olmuştur. Bu etki bir değişkenin öngörülen gücünün bir ölçüsüdür. Ana etki; bir girdinin, diğer girdilerin varyasyonunun ortalaması üzerindeki etkisi şeklinde ölçülmektedir. Bu düşünce; iki seviyeli bir deney için, aşağıdaki gibi cebirsel bir formüle yönlendiren faktörel deneyler durumunda sıklıkla uygulanmaktadır:
([X2,Y2] + [X2,Y1] – [X1,Y2] – [X2,Y1])/2
Daha genelleştirilmiş durumlar için, düzenli cebirsel bir ifade kolayca bulunamamaktadır. Bu zor durum için verileri en küçük kareler yöntemi ile hesaplamak faydalı olabilir.
f(x) = A + Bx
B çizgisinin eğimi = Dy / Dx.
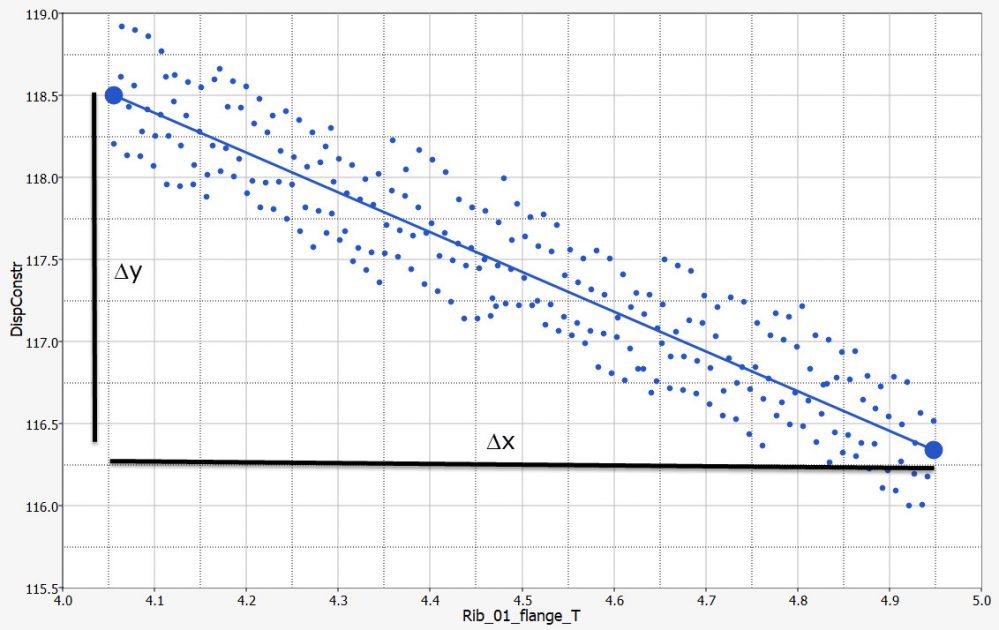
Sonuçta ortaya çıkan net değişiklik Dy, etkidir. Bu, doğrusal etkiyi regresyon katsayısı B ile temsil edebileceğimiz anlamına gelir:
Dy = BDx
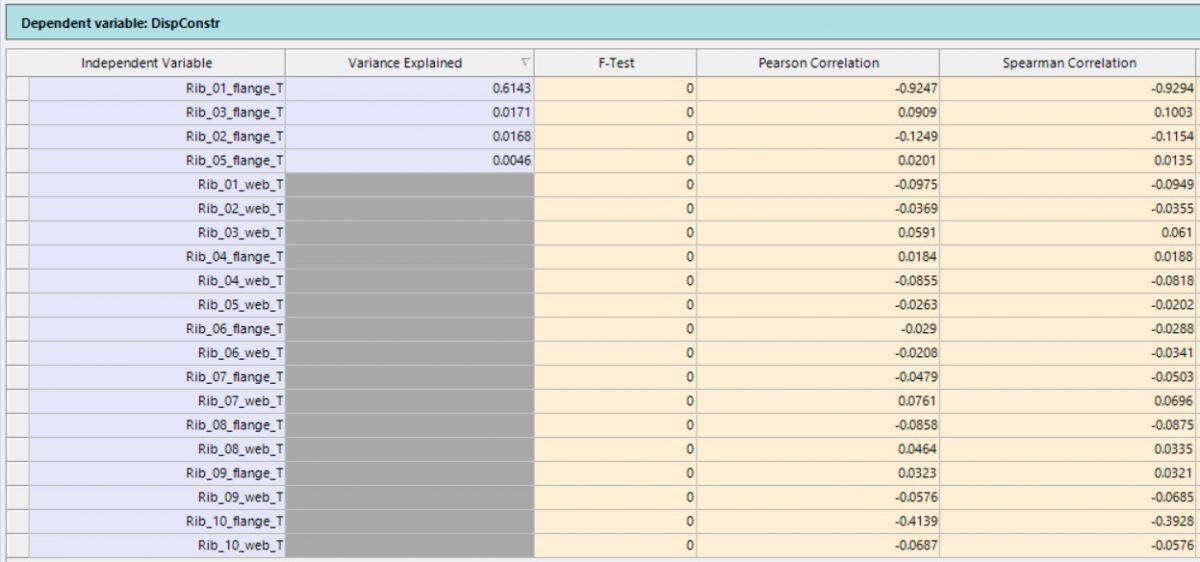
Bağımlı değişkenin, her bağımsız değişkenle ilişki derecesini ölçtükten sonra, etkiler bir tablo haline getirilebilmektedir.
Farklı öngörü gücüne sahip ölçüm setleri sonuçlarının, Altair Knowledge Studio’da gösterildiği gibi sınıflandırılabilir şekilde tablo haline getirilmesi, belirli bir çıktı için en etkili girdileri sıralamak için çok uygundur.
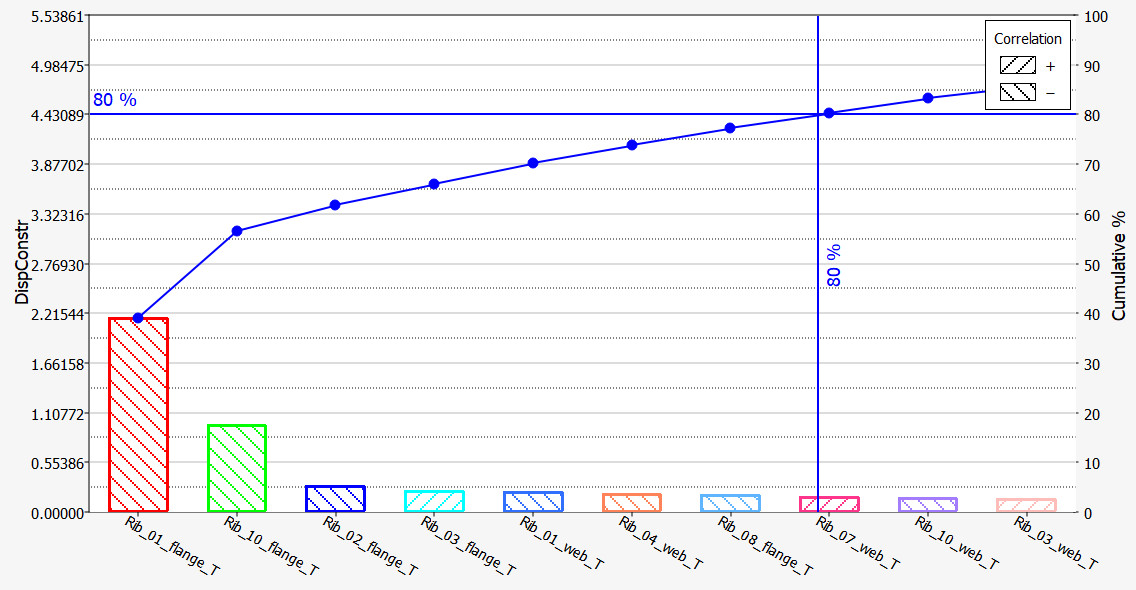
Alternatif olarak, bu aynı veriler Pareto grafiği olarak bilinen bir grafikte sunulabilmektedir. Bu grafik, girdilerin çıktılar üzerindeki etkilerini sütunlar şekilde büyükten küçüğe doğru sıralamaktadır. Ayrıca, girdinin çıktı üzerindeki etkisinin, pozitif veya negatif korelasyonunu açıklamaktadır. Grafik pareto ilkesi olarak da bilinen 80-20 kuralı ile ilgilidir. Çoğu olay için, etkilerin kabaca %80’inin etkenlerin %20’sinden kaynaklandığını belirtmektedir. Aşağıdaki Pareto grafiği, Altair HyperStudy‘den alınmıştır.
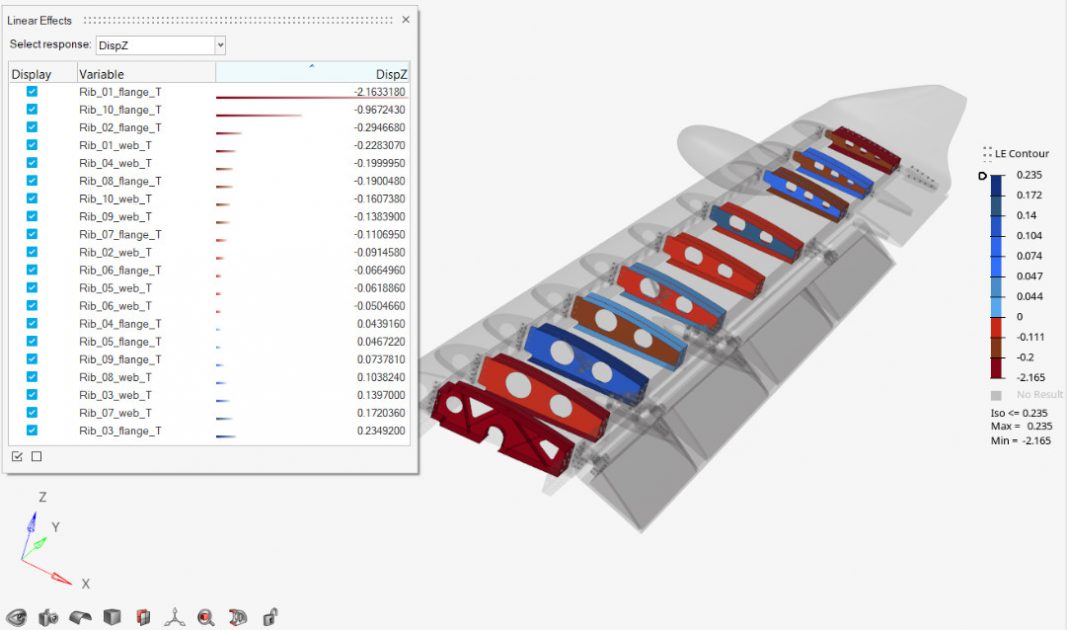
Aşağıdaki ekran görüntüsünde, veriler çok daha zengin bir şekilde görselleştirilmiştir.
Mühendislik tasarımlarında girdilerimiz genellikle fiziksel bir nesnenin kalınlık, malzeme, yarıçap, uzunluk gibi bazı özelliklerini temsil ettikleri için daha somut bir şekilde ifade edilebilmektedir. Sonucun bir 3D model üzerinde kontur olarak gösterilmesi soyut olarak düşünülen verilere hayat verebilmektedir. Örneğin, Altair HyperWorks’ten alınan aşağıdaki görüntü, yukarıdaki Pareto grafiği ile aynı verileri göstermektedir. Pozitif ve negatif korelasyonların büyüklüğü model üzerinde iki farklı renkte gösterilmektedir.
Bu, bilgi tasarımı ilkelerini kullanarak verilerin mühendislere nasıl sunulacağına dair sadece bir örnektir. Veri görselleştirme, bilim kadar sanat olabilen büyüleyici bir konudur.